
Eksempler på det gyldne snit kan findes over alt i klassisk arkitektur, kunst, natur og endda musik. Dette udtryk for proportioner, også kendt som det guddommelige forhold, tilbyder harmonisk komposition gennem anvendelsen af et irrationelt tal (1.618) i design, både naturligt og menneskeskabt. Mest sandsynligt er du ikke klar over matematikken bag det gyldne snits skønhed, fordi det producerer genstande og musik, som du naturligt vil finde tiltalende uden at skulle have nogen forklaring.
Golden Ratio in Architecture
The Golden Ratio skaber næsten perfekt skønhed i naturen og kunsten. Når du begynder at lede efter Golden Ratio-eksempler i hverdagen, kan du blive overrasket over de mange tilfælde, det er blevet brugt til at skabe mange monumentale bygninger og strukturer. Når det gyldne snit bruges i arkitektur, siges bygningen at være skabt ved at bruge "hellig arkitektur." Ved at anvende beregningen af det gyldne snit på en firkant er arkitekter og designere i stand til at skabe det gyldne rektangel, som menes at have de mest æstetisk tiltalende proportioner for det menneskelige øje.
Gyldent rektangel Eksempel: Parthenon

Phidias, den græske billedhugger, brugte det gyldne snit i sit arbejde, især da han begyndte at arbejde med de bånd, han skulpturerede lige over Parthenonsøjlerne. Det er også vigtigt at bemærke, at den numeriske værdi, der er tildelt det gyldne snit, Phi, blev navngivet til hans ære.
Hvis du måler dimensionerne af Parthenons ydre, vil du opdage, at den ikke kun danner et gyldent rektangel, men at der også er mange gyldne rektangler mellem søjlerne. Denne hellige struktur er et smukt eksempel på det gyldne snit i arkitekturen.
Den gyldne trekant Eksempel: Den store pyramide i Giza
Det gyldne snit, det gyldne rektangel og det gyldne trekant kan alle findes i perfektionen af et af verdens syv vidundere, den store pyramide i Giza. For at finde det gyldne snit skal du halvere pyramidens firkantede base og tegne en lodret linje op ad midten af pyramiden. Når denne er forbundet med en vinklet side af pyramiden, kan du nemt se, hvordan den danner den gyldne trekant med et forhold på 1,618, det gyldne snit.
Andre arkitektoniske eksempler
Du kan finde mange eksempler på gammel til moderne hellig arkitektur og bygninger med gyldne snit.
- Chartres Cathedral - Centre, Frankrig
- Notre Dame - Paris, Frankrig
- Porch of Maidens - Akropolis, Athen
- Taj Mahal - Agra, Indien
- United Nations Building - New York City, New York
Gyldent snit i kunsteksempler
Du kan finde mange eksempler af malere, der brugte det gyldne snit. Disse perfektionsværker blev skabt ved at bruge forholdet mellem gyldne rektangler og gyldne trekanter. Kunst skabt baseret på det gyldne rektangel viser sig at være mere behagelig for det menneskelige øje. Det er et af mysterierne, der omgiver dette perfekte rektangel og det gyldne snit.
Golden Ratio in Art

Kunsteksempler med det gyldne snit omfatter:
- Leonardo Di Vinci - Mona Lisa, Vitruvian Man
- Botticelli - Venus' fødsel
- Michelangelo - Holy Family, 'David'
- Raphael - Korsfæstelse
- Rembrandt - Selvportræt
- Salvador Dali - Nadverens sakramente, hukommelsens persistens
Using Golden Ratio i kunstkomposition
Inden for et gyldent rektangel er visse områder, der viser sig at være mere visuelt tiltalende end andre områder. Disse punkter opdages ved at tegne en linje fra det nederste hjørne af rektanglet til det modsatte hjørne og gentage det med det andet nederste hjørne. Disse linjer vil skære i det nøjagtige centrum af det gyldne rektangel. Mål derefter midtvejs langs hver linje, startende fra midtpunktet. Disse fire punkter kaldes rektanglets øjne (Golden Ratio). Maleriets hovedomdrejningspunkt tegnes eller males derefter inden for disse interessepunkter (forhold).
Golden Ratio in Music

Musik er sammensat af numerisk værdi, og når det gyldne snit bruges til at skabe et musikstykke, bliver det et levende eksempel på matematik. Fibonacci-sekvensen er også udbredt i musik:
- Der er otte toner i en skala.
- Tredje- og kvinttonen er grundlaget for akkorder.
- Længden eller oktaven af enhver node er 13 toner.
Sekvenseringen fortsætter gennem et stykke musik og bliver mere kompleks, efterhånden som det når det gyldne snit.
Komponister, der brugte det gyldne snit
Nogle af de mest kendte klassiske komponister brugte Golden Ratio og Fibonacci Sequencing i deres musikstykker, herunder Bach, Beethoven, Chopin og Mozart. Nogle moderne komponister som Casey Mongoven har udforsket det gyldne snit i deres musik.
Golden Ratio-eksempler i naturen

Hvor findes det gyldne snit i naturen? Det er i den gyldne eller fibonacci-spiral, som kan skabes ved at bruge det gyldne snit. Dette er et fænomen, der findes i vid udstrækning i den naturlige verden. En plantes blade vokser, så så mange som muligt kan spiralere op ad stilken. Et nyt blad dannes først, efter at det, der fortsætter, er dannet.
- Spiralkaktusser
- Spiralgalakser
- Solsikker
Blomster med Fibonacci-sekvensen
Nogle blomster har blomsterblade, der følger Fibonacci-sekvensen:
- Tre kronblade:Iris, lilje, orkideer, trillium
- Fem kronblade: Smørblomster, geranier, hibiscus, morning glory, nasturtium
- Otte kronblade: Delphiniums
- 13 kronblade: Visse sorter af tusindfryd, ragwort, morgenfrue
Fibonacci-spiral i fyrrekogler

Afhængigt af træarten kan du også se det gyldne snit i arbejde inden for en Fibonacci-talserie i fyrrekogler. Du kan finde en serie på otte spiraler på den ene side af fyrrekoglen, med 13 spiraler på den anden. Et andet fyrrekoglemønster har fem spiraler på den ene side med otte på den anden.
Golden Ratio in Humans
Dette forhold er også vigtigt for ikke kun hvordan mennesker ser på hinanden, men også for hvordan deres kroppe fungerer og i deres DNA.
DNA afslører det gyldne snit
Et af de mest fantastiske eksempler på Golden Ratio findes i den menneskelige DNA-struktur. Dette kan ses i et enkelt DNA-tværsnit, der afslører, at DNA-dobbelthelixen danner en tikantform. Dette er en kombination af to femkanter, roteret 36 grader fra hinanden, danner DNA-dobbelthelixen. Den dobbelte helix-spiral danner selv en femkant. Selv et enkelt DNA-molekyle afslører grundlaget for det gyldne snit eller den guddommelige proportion.
Matematikken bag det gyldne snit
At finde det gyldne snit i det virkelige liv er enkelt, da det ser ud over alt omkring dig. Det er en matematisk truisme, der bruges til at definere, hvad der almindeligvis er kendt som det perfekte tal, der findes i naturen, og som er blevet duplikeret og efterlignet af mennesker i århundreder. Den forsimplede skønhed ved dette nummer skjuler dets kompleksitet i udførelsen. For at forstå teorien bag det gyldne snit, skal du først udforske Fibonacci-sekvensen af forholdet.
Fibonacci-sekvensen og det gyldne snit
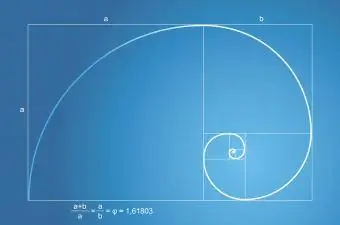
Fibonacci-sekvensen eller -serien har et forhold til det gyldne snit. Fibonacci-serien viser sig i antallet af blade på en plante og antallet af kronblade på en blomst. Fibonacci-spiralen, som findes i naturen, er altid en del af et gyldent rektangel med et gyldent snit.
Fibonacci-seriens matematik er enkel:
- Sekvensen begynder med 0 og 1.
- Bare læg de sidste to tal sammen for at få det næste tal i serien.
- 0+1=1, 1+1=2, 1+2=3, 2+3=5, 3+5=8, og så videre.
- Dette Fibonacci-eksempel bliver: 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 og så videre.
Fibonaccis forhold til det gyldne snit realiseres, når det tilføjes fremad, længere og længere. Jo mere du tilføjer serien, jo tættere kommer du på det gyldne snit.
Oprettelse af et gyldent rektangel og trekant
For at skabe et gyldent rektangel med Fibonacci-sekvensen starter du med en firkant. Du vil begynde at bygge et rektangel ved at tilføje endnu et kvadrat til det oprindelige kvadrat. Husk at bruge formlen: 0+1=1 er det første kvadrat, 1+1=2 - du tilføjer endnu et kvadrat.1+2=3 tilføjer du tre kvadrater, og derefter, 2+3=5, tilføjer du fem kvadrater. Du vil fortsætte med at tilføje firkanter og til sidst danne et gyldent rektangel.
En gylden trekant kan skabes ved at dele et gyldent rektangel i to fra det ene hjørne til det modsatte hjørne. Dette skaber en trekant, hvor dens tre sider eller vinkler har et forhold på 2:2:1, hvilket betyder, at de to lange sider er lige lange, og den korte vinkel er nøjagtigt halvdelen af længden af de to længere.
Golden Ratio i den virkelige verden
Det gyldne forhold omtales ofte som det guddommelige forhold på grund af dets fremtrædende plads i naturen og i menneskelige kroppe. Opdagelsen af, at det gyldne snit er til stede i så mange levende ting, fremmede en ærbødighed for denne magiske proportion, og den er fortsat en inspiration for kunstnere og skabere i dag.






